Self-Organizing Lists
📚 Drozdek (Ch. 3.5)
Skip lists were introduced to make searching more efficient ( \(O(\textrm{lg}(N))\) ), but require significant pointer overhead.
Searching in a singly-linked or doubly-linked list requires \(O(N)\) time.
But what if the value you are searching for is at (or near) the “front” of the list?
OK, but how do we do that?
🪄 ✨ Magic? ✨ ✨
Re-organize the values over time!
Self-Organizing Lists change the order of the values they contain so the values that are deemed more likely to be searched will appear nearer to the beginning of the list.
There are different ways to re-organize the list according to which values are searched for (and located). Here are the most common four:
Move-to-front method.
Transpose method.
Count method.
Ordering method.
Move-to-front method. Each time an element is located, it is immediately moved to the front of the list.
Transpose method. Each time an element is located, it is swapped with its immediate predecessor in the list (unless it is already at the front).
Count method. A count is stored in each node, indicating the number of times the node has been targeted by a search. The list is maintained in order by decreasing count; nodes are re-ordered after each successful search, which may require swapping the located node “forward” 1 or more times.
Ordering method. Order the list according to a criteria natural for the information being represented, so that values more likely to be searched would be stored nearer to the “front” of the list.

Stream: ACBCDADACACCEE
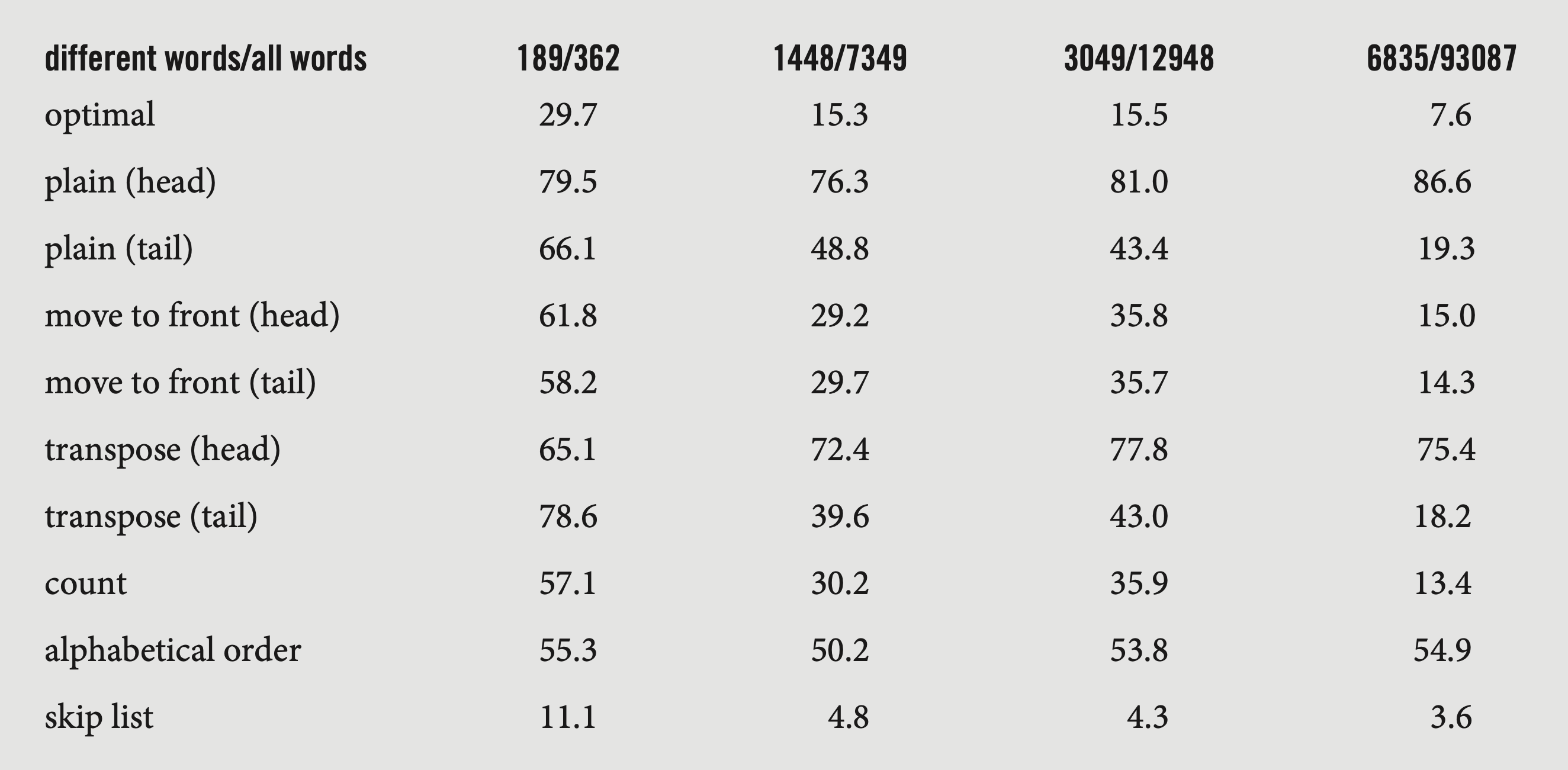
- Move-to-front and Count tend to outperform other re-organization methods.
- Adding at tail tends to outperform adding at head.
These sample runs show that for lists of modest size, the linked list suffices. With the increase in the amount of data and in the frequency with which they have to be accessed, more sophisticated methods and data structures need to be used. 1
Self-Organizing Lists

CS 50x2 Accelerated Programming Series